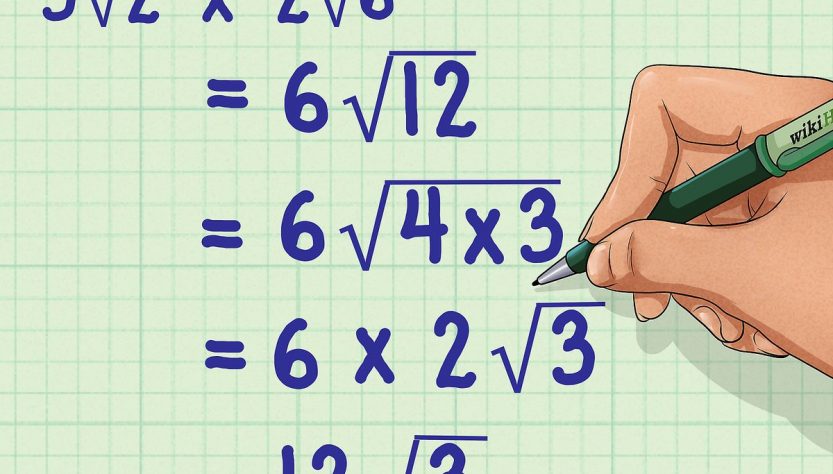Phép nhân căn bậc hai là gì? Cách nhân căn bậc hai, một dạng khai căn thường gặp, tương tự như cách nhân một số nguyên thông thường. Nhân căn bậc hai không phải là một dạng bài toán khó, tuy nhiên rất nhiều các bạn học sinh hay nhầm lẫn khi làm bài tập. Để giúp các em ghi nhớ kiến thức thật lâu và giải quyết các bài toán dễ dàng, Sau đây svnckh sẽ tổng hợp lại tất cả nội dung lý thuyết và kèm theo đó là bài tập thực hành liên quan. Mời các em học sinh và quý phụ huynh cùng tìm hiểu.
Nhân căn bậc hai có hệ số
1.Nhân phần hệ số với nhau.
Hệ số của căn bậc hai là số nằm bên ngoài dấu căn. Để nhân các hệ số với nhau, ta chỉ cần thực hiện phép nhân thông thường mà không xét đến phần có dấu căn. Tích của phép nhân này được đặt trước dấu căn thứ nhất.
Chú ý dấu (âm, dương) khi nhân hệ số. Đừng quên quy tắc tích của một số âm và một số dương là một số âm, và tích của hai số âm là một số dương.
Ví dụ ,
khi tính
![]()
Đầu tiên ta cần tính 3 x 2 = 6 Bài toán sẽ trở thành ![]()
Tìm hiểu thêm : Công thức cộng trừ nhân chia số nguyên
2. Nhân phần dưới dấu căn.
Như ở phần trước đã nêu, ta chỉ cần nhân phần dưới dấu căn như với các số nguyên thông thường. Hãy luôn nhớ ghi tích số thu được dưới dấu căn.

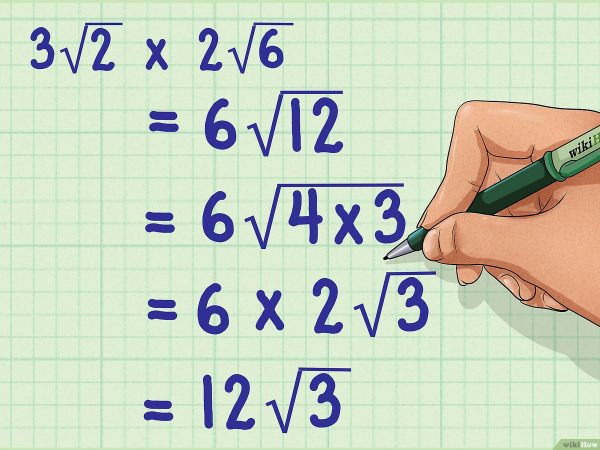
3. Rút gọn phần dưới căn thành tích của số chính phương.
Bước này sẽ giúp ta rút gọn đáp án. Nếu ta không thể tách ra từ phần dưới căn một số chính phương thì tức là đáp án tính được đã tối giản và ta có thể dừng tính toán tại đây.

4. Nhân căn bậc hai của số chính phương vừa tách với hệ số.
Phần còn lại đặt dưới dấu căn ta sẽ được kết quả rút gọn của phép tính.

Tìm hiểu thêm :Quy tắc cộng trừ nhân chia số tự nhiên
Nhân căn bậc hai không có hệ số
1.Nhân số khai căn với nhau.
Số khai căn là số nằm dưới dấu căn.Khi nhân số khai căn với nhau, ta tiến hành nhân như đối với số nguyên. Hãy nhớ ghi cả dấu căn vào phần kết quả
![]()
2. Viết phần dưới dấu căn dưới dạng tích của một số chính phương với một giá trị nguyên.
Để thực hiện bước này, ta cần xác định xem số khai căn có phải là bội của một số chính phương hay không.Nếu không thể rút ra được một số chính phương từ số khai căn thì tức là kết quả thu được đã ở dạng tối giản và ta không cần thực hiện thêm phép tính nào nữa.

3. Đặt căn bậc hai của số chính phương đã nhóm ra ngoài dấu căn.
Giữ nguyên phần còn lại dưới dấu căn. Đến đây ta đã tối giản được biểu thức căn.

4. Bình phương căn bậc hai.
Đôi khi ta cần phải lấy bình phương một căn bậc hai, hay nói cách khác, lấy căn bậc hai đó nhân với chính nó. Bình phương và khai căn một số là hai phép toán ngược nhau ; vì thế để làm mất dấu căn bậc hai, ta có thể bình phương chính nó. Kết quả của phép toán này chính là số nằm dưới dấu căn
![]()